R functions for the hierarchical shift function

The hierarchical shift function presented in the previous post is now available in the `rogme` R package. Here is a short demo.

Get the latest version of `rogme`:

# install.packages("devtools")
devtools::install_github("GRousselet/rogme")
library(rogme)
library(tibble)

Load data and compute hierarchical shift function:

df <- flp # get reaction time data - for details `help(flp)`
# Compute shift functions for all participants
out <- hsf(df, rt ~ condition + participant)

Because of the large number of participants, the confidence intervals are too narrow to be visible. So let’s subset a random sample of participants to see what can happen with a more smaller sample size:

set.seed(22) # subset random sample of participants
id <- unique(df$participant) 
df <- subset(df, flp$participant %in% sample(id, 50, replace = FALSE))
out <- hsf(df, rt ~ condition + participant) 
plot_hsf(out)

Want to estimate the quartiles only?

out <- hsf(df, rt ~ condition + participant, qseq = c(.25, .5, .75))
plot_hsf(out)

Want to reverse the comparison?

out <- hsf(df, rt ~ condition + participant, todo = c(2,1))
plot_hsf(out)

P values are here:

out$pvalues

P values adjusted for multiple comparisons using Hochberg’s method:

out$adjusted_pvalues 

Percentile bootstrap version:

set.seed(8899)
out <- hsf_pb(df, rt ~ condition + participant)

Plot bootstrap highest density intervals – default:

plot_hsf_pb(out) 

Plot distributions of bootstrap samples of group differences. Bootstrap distributions are shown in orange. Black dot marks the mode. Vertical black lines mark the 50% and 90% highest density intervals.

plot_hsf_pb_dist(out)

 

For more examples, a vignette is available on GitHub.

Feedback would be much appreciated: don’t hesitate to leave a comment or to get in touch directly.

Hierarchical shift function: a powerful alternative to the t-test

In this post I introduce a simple yet powerful method to compare two dependent groups: the hierarchical shift function. The code is on GitHub. More details are in Rousselet & Wilcox (2019), with a reproducibility package on figshare.

Let’s consider different situations in a hierarchical setting: we’ve got trials from 2 conditions in several participants. Imagine we collected data from one participant and the results look like this:

These fake reaction time data were created by sampling from ex-Gaussian distributions. Here the two populations are shifted by a constant, so we expect a uniform shift between the two samples. Later we’ll look at examples showing  differences most strongly in early responses, late responses, and in spread.

To better understand how the distributions differ, let’s look at a shift function, in which the difference between the deciles of the two conditions are plotted as a function of the deciles in condition 1 – see details in Rousselet et al. (2017). The decile differences are all negative, showing stochastic dominance of condition 2 over condition 1. The function is not flat because of random sampling and limited sample size. 

Now, let’s say we collected 100 trials per condition from 30 participants. How do we proceed? There are a variety of approaches available to quantify distribution differences. Ideally, such data would be analysed using a multi-level model, including for instance ex-Gaussian fits, random slopes and intercepts for participants, item analyses… This can be done using the lme4 or brms R packages. However, in my experience, in neuroscience and psychology articles, the most common approach is to collapse the variability across trials into a single number per participant and condition to be able to perform a paired t-test: typically, the mean is computed across trials for each condition and participant, then the means are subtracted, and the distribution of mean differences is entered into a one-sample t-test. Obviously, this strategy throws away a huge amount of information! And the results of such second-tier t-tests are difficult to interpret: a positive test leaves us wondering exactly how the distributions differ; a negative test is ambiguous – beside avoiding the ‘absence of evidence is not evidence of absence’ classic error, we also need to check if the distributions do not differ in other aspects than the mean. So what can we do?

Depending on how conditions differ, looking at other aspects of the data than the mean can be more informative. For instance, in Rousselet & Wilcox (2019), we consider group comparisons of individual medians. Considering that the median is the second quartile, looking at the other quartiles can be of theoretical interest to investigate effects in early or later parts of distributions. This could be done in several ways, for instance by making inferences on the first quartile (Q1) or the third quartile (Q3). If the goal is to detect differences anywhere in the distributions, a more systematic approach consists in quantifying differences at multiple quantiles. Here we consider the case of the deciles, but other quantiles could be used. First, for each participant and each condition, the sample deciles are computed over trials. Second, for each participant, condition 2 deciles are subtracted from condition 1 deciles – we’re dealing with a within-subject (repeated-measure) design. Third, for each decile, the distribution of differences is subjected to a one-sample test. Fourth, a correction for multiple comparisons is applied across the 9 one-sample tests. I call this procedure a hierarchical shift function. There are many options available to implement this procedure and the example used here is not the definitive answer: the goal is simply to demonstrate that a relatively simple procedure can be much more powerful and informative than standard approaches.

In creating a hierarchical shift function we need to make three choices: a quantile estimator, a statistical test to assess quantile differences across participants, and a correction for multiple comparisons technique. The deciles were estimated using type 8 from the base R quantile() function (see justification in Rousselet & Wilcox, 2019). The group comparisons were performed using a one-sample t-test on 20% trimmed means, which performs well in many situations, including in the presence of outliers. The correction for multiple comparisons employed Hochberg’s strategy (Hochberg, 1988), which guarantees that the probability of at least one false positive will not exceed the nominal level as long as the nominal level is not exceeded for each quantile. 

In Rousselet & Wilcox (2019), we consider power curves for the hierarchical shift function (HSF) and contrast them to other approaches: by design, HSF is sensitive to more types of differences than any standard approach using the mean or a single quantile. Another advantage of HSF is that the location of the distribution difference can be interrogated, which is impossible if inferences are limited to a single value.

Here is what the hierarchical shift function looks like for our uniform shift example:

The decile differences between conditions are plotted for each participant (colour coded) and the group 20% trimmed means are superimposed in black. Differences are pretty constant across deciles, suggesting a uniform shift. Most participants have shift functions entirely negative – a case of stochastic dominance of one condition over the other. There is growing uncertainty as we consider higher deciles, which is expected from measurements of right skewed distributions.

We can add confidence intervals:

P values are available in the GitHub code.

Instead of standard parametric confidence intervals, we can also consider percentile bootstrap confidence intervals (or highest density intervals), as done here:

Distributions of bootstrap estimates can be considered cheap Bayesian posterior distributions. They also contain useful information not captured by simply reporting confidence intervals.

Here we plot them using geom_halfeyeh() from tidybayes. 

The distributions of bootstrap estimates of the group 20% trimmed means are shown in orange, one for each decile. Along the base of each distribution, the black dot marks the mode and the vertical lines mark the 50% and 90% highest density intervals.

Nice hey?! Reporting a figure like that is dramatically more informative than reporting a P value and a confidence interval from a t-test!

A bootstrap approach can also be used to perform a cluster correction for multiple comparisons – see details on GitHub. Preliminary simulations suggest that the approach can provide substantial increase in power over the Hochberg’s correction – more on that in another post.

Let’s look at 3 more examples, just for fun…

Example 2: early difference

Example participant:

Shift function:

Hierarchical shift function with confidence intervals:

Percentile bootstrap estimate densities:

Example 3: difference in spread

Example participant:

Shift function:

Hierarchical shift function with confidence intervals:

Percentile bootstrap estimate densities:

Example 4: late difference

Example participant:

Shift function:

Hierarchical shift function with confidence intervals:

Percentile bootstrap estimate densities:

Conclusion

The hierarchical shift function can be used to achieve two goals: 

• to screen data for potential distribution differences using p values, without limiting the exploration to a single statistics like the mean;
• to illustrate and quantify how distributions differ.

I think of the hierarchical shift function as the missing link between t-tests and multi-level models. I hope it will help a few people make sense of their data and maybe nudge them towards proper hierarchical modelling.

R functions for the parametric hierarchical shift function are available in the rogme package. I also plan bootstrap functions. Then I’ll tackle the case of 2 independent groups, which requires a third level quantifying differences of differences.

 

Illustration of continuous distributions using quantiles

In this post I’m going to show you a few simple steps to illustrate continuous distributions. As an example, we consider reaction time data, which are typically positively skewed and can differ in different ways. Reaction time distributions are also a rich source of information to constrain cognitive theories and models. So unless the distributions are at least illustrated, this information is lost (which is typically the case when distributions are summarised using a single value like the mean). Other approaches not covered here include explicit mathematical models of decision making and fitting functions to model the shape of the distributions (Balota & Yap, 2011).

For our current example, I made up data for 2 independent groups with four patterns of differences:

• no clear differences;

• uniform shift between distributions;

• mostly late differences;

• mostly early differences.

The R code is on GitHub.

Scatterplots

For our first visualisation, we use geom_jitter() from ggplot2. The 1D scatterplots give us a good idea of how the groups differ but they’re not the easiest to read. The main reason is probably that we need to estimate local densities of points in different regions and compare them between groups.

For the purpose of this exercise, each group (g1 and g2) is composed of 1,000 observations, so the differences in shapes are quite striking. With smaller sample sizes the evaluation of these graphs could be much more challenging.

Kernel density plots

Relative to scatterplots, I find that kernel density plots make the comparisons between groups much easier.

Improved scatterplots

Scatterplots and kernel density plots can be combined by using beeswarm plots. Here we create scatterplots shaped by local density using the geom_quasirandom() function from the ggbeeswarm package. Essentially, the function creates violin plots in which the constituent points are visible. 

To make the plots even more informative, I’ve superimposed quantiles – here deciles computed using the Harrell-Davis quantile estimator. The deciles are represented by vertical black lines, with medians shown with thicker lines. Medians are informative about the location of the bulk of the observations and comparing the lower to upper quantiles let us appreciate the amount of asymmetry within distributions. Comparing quantiles between groups give us a sense of the amount of relative compression/expansion on each side of the distributions. This information would be lost if we only compared the medians. 

Quantile plots

If we remove the scatterplots and only show the quantiles, we obtain quantile plots, which provide a compact description of how distributions differ (please post a comment if you know of older references using quantile plots). Because the quantiles are superimposed, they are easier to compare than in the previous scatterplots. To help with the group comparisons, I’ve also added plots of the quantile differences, which emphasise the different patterns of group differences.

Vincentile plots

An alternative to quantiles are Vincentiles, which are computed by sorting the data and splitting them in equi-populated bins (there is the same number of observations in each bin). Then the mean is computed for each bin (Balota et al. 2008; Jiang et al. 2004). Below means were computed for 9 equi-populated bins. As expected from the way they are computed, quantile plots and Vincentile plots look very similar for our large samples from continuous variables.

Group quantile and Vincentile plots can be created by averaging quantiles and Vincentiles across participants (Balota & Yap, 2011; Ratcliff, 1979). This will be the topic of another post.

Delta plots

Related to quantile plots and Vincentile plots, delta plots show the difference between conditions, bin by bin (for each Vincentile) along the y-axis, as a function of the mean across conditions for each bin along the x-axis (De Jong et al., 1994). Not surprisingly, these plots have very similar shapes to the quantile difference plots we considered earlier. 

Negative delta plots (nDP, delta plots with a negative slope) have received particular attention because of their theoretical importance (Ellinghaus & Miller, 2018; Schwarz & Miller, 2012).

Shift function

Delta plots are related to the shift function, a powerful tool introduced in the 1970s: it consists in plotting the difference between the quantiles of two groups as a function of the quantiles in one group, with some measure of uncertainty around the difference (Doksum, 1974; Doksum & Sievers, 1976; Doksum, 1977). It was later refined by Rand Wilcox (Rousselet et al. 2017). This modern version is shown below, with deciles estimated using the Harrell-Davis quantile estimator, and percentile bootstrap confidence intervals of the quantile differences. The sign of the difference is colour-coded (purple for negative, orange for positive).

Unlike other graphical quantile techniques presented here, the shift function affords statistical inferences because of it’s use of confidence intervals (the shift function also comes in a few Bayesian flavours). It is probably one of the easiest ways to compare entire distributions, without resorting to explicit models of the distributions. But the shift function and the other graphical methods demonstrated in this post are not meant to compete with hierarchical models. Instead, they can be used to better understand data patterns within and between participants, before modelling attempts. They also provide powerful alternatives to the mindless application of t-tests and bar graphs, helping to nudge researchers away from the unique use of the mean (or the median) and towards considering the rich information available in continuous distributions.

References

Balota, D.A. & Yap, M.J. (2011) Moving Beyond the Mean in Studies of Mental Chronometry: The Power of Response Time Distributional Analyses. Curr Dir Psychol Sci, 20, 160-166.

Balota, D.A., Yap, M.J., Cortese, M.J. & Watson, J.M. (2008) Beyond mean response latency: Response time distributional analyses of semantic priming. J Mem Lang, 59, 495-523.

Clarke, E. & Sherrill-Mix, S. (2016) ggbeeswarm: Categorical Scatter (Violin Point) Plots.

De Jong, R., Liang, C.C. & Lauber, E. (1994) Conditional and Unconditional Automaticity – a Dual-Process Model of Effects of Spatial Stimulus – Response Correspondence. J Exp Psychol Human, 20, 731-750.

Doksum, K. (1974) Empirical Probability Plots and Statistical Inference for Nonlinear Models in the two-Sample Case. Ann Stat, 2, 267-277.

Doksum, K.A. (1977) Some graphical methods in statistics. A review and some extensions. Statistica Neerlandica, 31, 53-68.

Doksum, K.A. & Sievers, G.L. (1976) Plotting with Confidence – Graphical Comparisons of 2 Populations. Biometrika, 63, 421-434.

Ellinghaus, R. & Miller, J. (2018) Delta plots with negative-going slopes as a potential marker of decreasing response activation in masked semantic priming. Psychol Res, 82, 590-599.

Jiang, Y., Rouder, J.N. & Speckman, P.L. (2004) A note on the sampling properties of the Vincentizing (quantile averaging) procedure. J Math Psychol, 48, 186-195.

Ratcliff, R. (1979) Group Reaction-Time Distributions and an Analysis of Distribution Statistics. Psychol Bull, 86, 446-461.

Rousselet, G.A., Pernet, C.R. & Wilcox, R.R. (2017) Beyond differences in means: robust graphical methods to compare two groups in neuroscience. The European journal of neuroscience, 46, 1738-1748.

Schwarz, W. & Miller, J. (2012) Response time models of delta plots with negative-going slopes. Psychon B Rev, 19, 555-574.

Correlations in neuroscience: are small n, interaction fallacies, lack of illustrations and confidence intervals the norm?

As reviewer, editor and reader of research articles, I’m regularly annoyed by the low standards in correlation analyses. In my experience with such articles, typically:

• Pearson’s correlation, a non-robust measure of association, is used;
• R and p values are reported, but not confidence intervals;
• sample sizes tend to be small, leading to large estimation bias and inflated effect sizes in the literature;
• R values and confidence intervals are not considered when interpreting the results;
• instead, most analyses are reported as significant or non-significant (p<0.05), leading to the conclusion that an association exists or not (frequentist fallacy);
• often figures illustrating the correlations are absent;
• the explicit or implicit comparison of two correlations is done without a formal test (interaction fallacy).

To find out if my experience was in fact representative of the typical paper, I had a look at all papers published in 2017 in the European Journal of Neuroscience, where I’m a section editor. I care about the quality of the research published in EJN, so this is not an attempt at blaming a journal in particular, rather it’s a starting point to address a general problem. I really hope the results presented below will serve as a wake-up call for all involved and will lead to improvements in correlation analyses. Also, I bet if you look systematically at articles published in other neuroscience journals you’ll find the same problems. If you’re not convinced, go ahead, prove me wrong 😉 

I proceeded like this: for all 2017 articles (volumes 45 and 46), I searched for “correl” and I scanned for figures of scatterplots. If either searches were negative, the article was categorised as not containing a correlation analysis, so I might have missed a few. When at least one correlation was present, I looked for these details: 

• n
• estimator
• confidence interval
• R
• p value
• consideration of effect sizes
• figure illustrating positive result
• figure illustrating negative result
• interaction test.

164 articles reported no correlation.

7 articles used regression analyses, with sample sizes as low as n=6, n=10, n=12 in 3 articles.

48 articles reported correlations.

Sample size

The norm was to not report degrees of freedom or sample size along with the correlation analyses or their illustrations. In 7 articles, the sample sizes were very difficult or impossible to guess. In the others, sample sizes varied a lot, both within and between articles. To confirm sample sizes, I counted the observations in scatterplots when they were available and not too crowded – this was a tedious job and I probably got some estimations and checks wrong. Anyway, I shouldn’t have to do all these checks, so something went wrong during the reviewing process. 

To simplify the presentation of the results, I collapsed the sample size estimates across articles. Here is the distribution: 

The figure omits 3 outliers with n= 836, 1397, 1407, all from the same article.

The median sample size is 18, which is far too low to provide sufficiently precise estimation.

Estimator

The issue with low sample sizes is made worse by the predominant use of Pearson’s correlation or the lack of consideration for the type of estimator. Indeed, 21 articles did not mention the estimator used at all, but presumably they used Pearson’s correlation.

Among the 27 articles that did mention which estimator was used:

• 11 used only Pearson’s correlation;
• 11 used only Spearman’s correlation;
• 4 used Pearson’s and Spearman’s correlations;
• 1 used Spearman’s and Kendall’s correlations.

So the majority of studies used an estimator that is well-known for its lack of robustness and its inaccurate confidence intervals and p values (Pernet, Wilcox & Rousselet, 2012).

R & p values

Most articles reported R and p values. Only 2 articles did not report R values. The same 2 articles also omitted p values, simply mentioning that the correlations were not significant. Another 3 articles did not report p values along with the R values.

Confidence interval

Only 3 articles reported confidence intervals, without mentioning how they were computed. 1 article reported percentile bootstrap confidence intervals for Pearson’s correlations, which is the recommended procedure for this estimator (Pernet, Wilcox & Rousselet, 2012).

Consideration for effect sizes

Given the lack of interest for measurement uncertainty demonstrated by the absence of confidence intervals in most articles, it is not surprising that only 5 articles mentioned the size of the correlation when presenting the results. All other articles simply reported the correlations as significant or not.

Illustrations

In contrast with the absence of confidence intervals and consideration for effect sizes, 23 articles reported illustrations for positive results. 4 articles reported only negative results, which leaves us with 21 articles that failed to illustrate the correlation results. 

Among the 40 articles that reported negative results, only 13 illustrated them, which suggests a strong bias towards positive results.

Interaction test

Finally, I looked for interaction fallacies (Nieuwenhuis, Forstmann & Wagenmakers 2011). In the context of correlation analyses, you commit an interaction fallacy when you present two correlations, one significant, the other not, implying that the 2 differ, but without explicitly testing the interaction. In other versions of the interaction fallacy, two significant correlations with the same sign are presented together, implying either that the 2 are similar, or that one is stronger than the other, without providing a confidence interval for the correlation difference. You can easily guess the other flavours… 

10 articles presented only one correlation, so there was no scope for the interaction fallacy. Among the 38 articles that presented more than one correlation, only one provided an explicit test for the comparison of 2 correlations. However, the authors omitted the explicit test for their next comparison!

Recommendations

In conclusion, at least in 2017 EJN articles, the norm is to estimate associations using small sample sizes and a non-robust estimator, to not provide confidence intervals and to not consider effect sizes and measurement uncertainty when presenting the results. Also, positive results are more likely to be illustrated than negative ones. Finally, interaction fallacies are mainstream.

How can we do a better job?

If you want to do a correlation analysis, consider your sample size carefully to assess statistical power and even better, your long-term estimation precision. If you have a small n, I wouldn’t even look at the correlation. 

Do not use Pearson’s correlation unless you have well-behaved and large samples, and you are only interested in linear relationships; otherwise explore robust measures of associations and techniques that provide valid confidence intervals (Pernet, Wilcox & Rousselet, 2012; Wilcox & Rousselet, 2018).

Reporting

These details are essential in articles reporting correlation analyses:

• sample size for each correlation;
• estimator of association;
• R value;
• confidence interval;
• scatterplot illustration of every correlation, irrespective of the p value;
• explicit comparison test of all correlations explicitly or implicitly compared;
• consideration of effect sizes (R values) and their uncertainty (confidence intervals) in the interpretation of the results.

 Report p values if you want but they are not essential and should not be given a special status (McShane et al. 2018).

Finally, are you sure you really want to compute a correlation?

“Why then are correlation coefficients so attractive? Only bad reasons seem to come to mind. Worst of all, probably, is the absence of any need to think about units for either variable. Given two perfectly meaningless variables, one is reminded of their meaninglessness when a regression coefficient is given, since one wonders how to interpret its value. A correlation coefficient is less likely to bring up the unpleasant truth—we think we know what r = —.7 means. Do we? How often? Sweeping things under the rug is the enemy of good data analysis. Often, using the correlation coefficient is “sweeping under the rug” with a vengeance. Being so disinterested in our variables that we do not care about their units can hardly be desirable.”
Analyzing data: Sanctification or detective work?

John W. Tukey.
 American Psychologist, Vol 24(2), Feb 1969, 83-91. http://dx.doi.org/10.1037/h0027108

 

References

McShane, B.B., Gal, D., Gelman, A., Robert, C. & Tackett, J.L. (2018) Abandon Statistical Significance. arxiv.

Nieuwenhuis, S., Forstmann, B.U. & Wagenmakers, E.J. (2011) Erroneous analyses of interactions in neuroscience: a problem of significance. Nat Neurosci, 14, 1105-1107.

Pernet, C.R., Wilcox, R. & Rousselet, G.A. (2012) Robust correlation analyses: false positive and power validation using a new open source matlab toolbox. Front Psychol, 3, 606.

Rousselet, G.A. & Pernet, C.R. (2012) Improving standards in brain-behavior correlation analyses. Frontiers in human neuroscience, 6, 119.

Wilcox, R.R. & Rousselet, G.A. (2018) A Guide to Robust Statistical Methods in Neuroscience. Curr Protoc Neurosci, 82, 8 42 41-48 42 30.

[preprint]

A clearer explanation of the shift function

The shift function is a power tool to compare two marginal distributions. It’s covered in detail in this previous post. Below is a new illustration which might help better understand the graphical representation of the shift function. The R code to generate the figure is available in the README of the rogme package.

Panel A illustrates two distributions, both n = 1000, that differ in spread. The observations in the scatterplots were jittered based on their local density, as implemented in ggforce::geom_sina.

Panel B illustrates the same data from panel A. The dark vertical lines mark the deciles of the distributions. The thicker vertical line in each distribution is the median. Between distributions, the matching deciles are joined by coloured lined. If the decile difference between group 1 and group 2 is positive, the line is orange; if it is negative, the line is purple. The values of the differences for deciles 1 and 9 are indicated in the superimposed labels.

Panel C focuses on the portion of the x-axis marked by the grey shaded area at the bottom of panel B. It shows the deciles of group 1 on the x-axis – the same values that are shown for group 1 in panel B. The y-axis shows the differences between deciles: the difference is large and positive for decile 1; it then progressively decreases to reach almost zero for decile 5 (the median); it becomes progressively more negative for higher deciles. Thus, for each decile the shift function illustrates by how much one distribution needs to be shifted to match another one. In our example, we illustrate by how much we need to shift deciles from group 2 to match deciles from group 1.

More generally, a shift function shows quantile differences as a function of quantiles in one group. It estimates how and by how much two distributions differ. It is thus a powerful alternative to the traditional t-test on means, which focuses on only one, non-robust, quantity. Quantiles are robust, intuitive and informative.

Problems with small sample sizes

In psychology and neuroscience, the typical sample size is too small. I’ve recently seen several neuroscience papers with n = 3-6 animals. For instance, this article uses n = 3 mice per group in a one-way ANOVA. This is a real problem because small sample size is associated with:

• low statistical power

• inflated false discovery rate

• inflated effect size estimation

• low reproducibility

• …

Here is a list of excellent publications covering these points:

Button, K.S., Ioannidis, J.P., Mokrysz, C., Nosek, B.A., Flint, J., Robinson, E.S. & Munafo, M.R. (2013) Power failure: why small sample size undermines the reliability of neuroscience. Nature reviews. Neuroscience, 14, 365-376.

Colquhoun, D. (2014) An investigation of the false discovery rate and the misinterpretation of p-values. R Soc Open Sci, 1, 140216.

Forstmeier, W., Wagenmakers, E.J. & Parker, T.H. (2016) Detecting and avoiding likely false-positive findings – a practical guide. Biol Rev Camb Philos Soc.

Lakens, D., & Albers, C. J. (2017, September 10). When power analyses based on pilot data are biased: Inaccurate effect size estimators and follow-up bias. Retrieved from psyarxiv.com/b7z4q

See also these two blog posts on small n:

When small samples are problematic

Low Power & Effect Sizes

Small sample size also prevents us from properly estimating and modelling the populations we sample from. As a consequence, small n stops us from answering a fundamental, yet often ignored empirical question: how do distributions differ?

This important aspect is illustrated in the figure below. Columns show distributions that differ in four different ways. The rows illustrate samples of different sizes. The scatterplots were jittered using ggforce::geom_sina in R. The vertical black bars indicate the mean of each sample. In row 1, examples 1, 3 and 4 have exactly the same mean. In example 2 the means of the two distributions differ by 2 arbitrary units. The remaining rows illustrate random subsamples of data from row 1. Above each plot, the t value, mean difference and its confidence interval are reported. Even with 100 observations we might struggle to approximate the shape of the parent population. Without additional information, it can be difficult to determine if an observation is an outlier, particularly for skewed distributions. In column 4, samples with n = 20 and n = 5 are very misleading.

Small sample size could be less of a problem in a Bayesian framework, in which information from prior experiments can be incorporated in the analyses. In the blind and significance obsessed frequentist world, small n is a recipe for disaster.

Matlab code for the shift function: a powerful tool to compare two entire marginal distributions

Recently, I presented R code for the shift function, a powerful tool to compare two entire marginal distributions.

The Matlab code is now available on github.

shifthd has the same name as its R version, which was originally programmed by Rand Wilcox and first documented in 1995 (see details ). It computes a shift function for independent groups, using a percentile bootstrap estimation of the SE of the quantiles to compute confidence intervals.

shiftdhd is the version for dependent groups.

More recently, Wilcox introduced a new version of the shift function in which a straightforward percentile bootstrap is used to compute the confidence intervals, without estimation of the SE of the quantiles. This is implemented in Matlab as shifthd_pbci for independent groups (equivalent to qcomhd in R); as shiftdhd_pbci for dependent groups (equivalent to Dqcomhd in R).

A demo file shift_function_demo is available here, along with the function shift_fig and dependencies cmu and UnivarScatter.

For instance, if we use the ozone data covered in the previous shift function post, a call to shifthd looks like this:

[xd, yd, delta, deltaCI] = shifthd(control,ozone,200,1);

producing this figure:

The output of shifthd, or any of the other 3 sf functions, can be used as input into shift_fig:

shift_fig(xd, yd, delta, deltaCI,control,ozone,1,5);

producing this figure:

This is obviously work in progress, and shift_fig is meant as a starting point.

Have fun exploring how your distributions differ!

And if you have any question, don’t hesitate to get in touch.

A few simple steps to improve the description of neuroscience group results

---

This post is a draft of an editorial letter I’m writing for the European Journal of Neuroscience. It builds on previous posts on visualisation of behavioural and ERP data.

---

Update 2016-09-16: the editorial is now accepted:

Rousselet, G. A., Foxe, J. J. and Bolam, J. P. (2016), A few simple steps to improve the description of group results in neuroscience. Eur J Neurosci. Accepted Author Manuscript. doi:10.1111/ejn.13400

The final illustrations are available on Figshare: Rousselet, G.A. (2016): A few simple steps to improve the description of group results in neuroscience. figshare. https://dx.doi.org/10.6084/m9.figshare.3806487

---

 

 

There are many changes necessary to improve the quality of neuroscience research. Suggestions abound to increase openness, promote better experimental designs and analyses, and educate researchers about statistical inferences. These changes are necessary and will take time to implement. As part of this process, here, we would like to propose a few simple steps to improve the assessment of statistical results in neuroscience, by focusing on detailed graphical representations.

Despite a potentially sophisticated experimental design, in a typical neuroscience experiment, raw continuous data tend to undergo drastic simplifications. As a result, it is common for the main results of an article to be summarised in a few figures and a few statistical tests. Unfortunately, graphical representations in many scientific journals, including neuroscience journals, tend to hide underlying distributions, with their excessive use of line and bar graphs (Allen et al., 2012; Weissgerber et al., 2015). This is problematic because common basic summary statistics, such as mean and standard deviation are not robust and do not provide enough information about a distribution, and can thus give misleading impressions about a dataset, particularly for the small sample sizes we are accustomed to in neuroscience (Anscombe, 1973; Wilcox, 2012). As a consequence of poor data representation, there can be a mismatch between the outcome of statistical tests, their interpretations, and the information available in the raw data distributions.

Let’s consider a general and familiar scenario in which observations from two groups of participants are summarised using a bar graph, and compared using a t-test on means. If the p value is inferior to 0.05, we might conclude that we have a significant effect, with one group having larger values than the other one; if the p value is not inferior to 0.05, we might conclude that the two distributions do not differ. What is wrong with this description? In addition to the potentially irrational use of p values (Gigerenzer, 2004; Wagenmakers, 2007; Wetzels et al., 2011), the situation above highlights many caveats in current practices. Indeed, using bar graphs and an arbitrary p<0.05 cut-off turns a potentially rich pattern of results into a simplistic, binary outcome, in which effect sizes and individual differences are ignored. For instance, a more fruitful approach to describing a seemingly significant group effect would be to answer these questions as well:

• how many participants show an effect in the same direction as the group? It is possible to get significant group effects with very few individual participants showing a significant effect themselves. Actually, with large enough sample sizes you can pretty much guarantee significant group effects (Wagenmakers, 2007);

• how many participants show no effect, or an effect in the opposite direction as the group?

• is there a smooth continuum of effects across participants, or can we identify sub-clusters of participants who appear to behave differently from the rest?

• how large are the individual effects?

These questions can only be answered by using scatterplots or other detailed graphical representations of the results, and by reporting other quantities than the mean and standard deviation of each group. Essentially, a significant t-test is neither necessary nor sufficient to understand how two distributions differ (Wilcox, 2006). And because t-tests and ANOVAs on means are not robust (for instance to skewness & outliers), failure to reach the 0.05 cut-off should not be used to claim that distributions do not differ: first, the lack of significance (p<0.05) is not the same as evidence for the lack of effect (Kruschke, 2013); second, robust statistical tests should be considered (Wilcox, 2012); third, distributions can potentially differ in their left or right tails, but not in their central tendency, for instance when only weaker animals respond to a treatment (Doksum, 1974; Doksum & Sievers, 1976; Wilcox, 2006; Wilcox et al., 2014). Essentially, if an article reports bar graphs and non-significant statistical analyses of the mean, not much can be concluded at all. Without detailed and informative illustrations of the results, it is impossible to tell if the distributions truly do not differ.

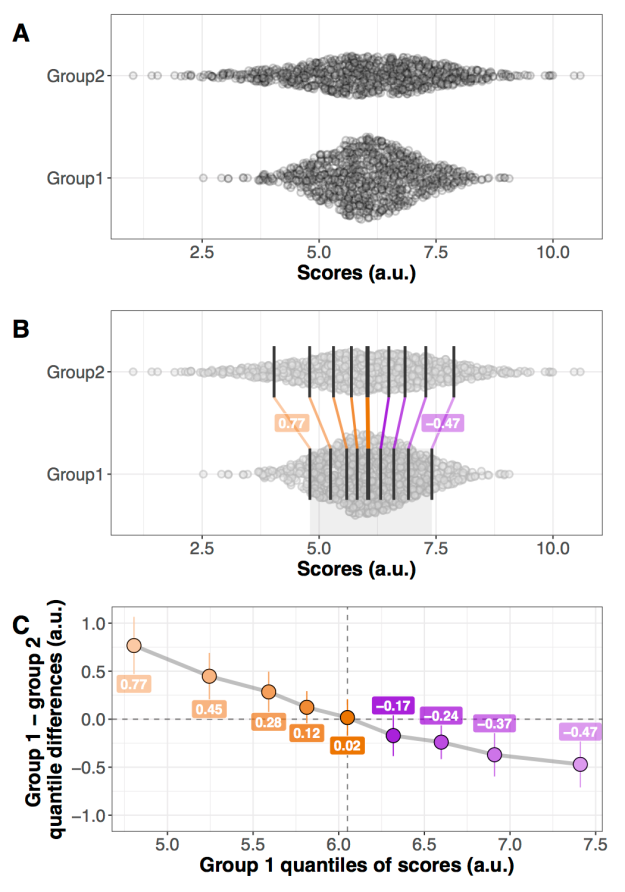
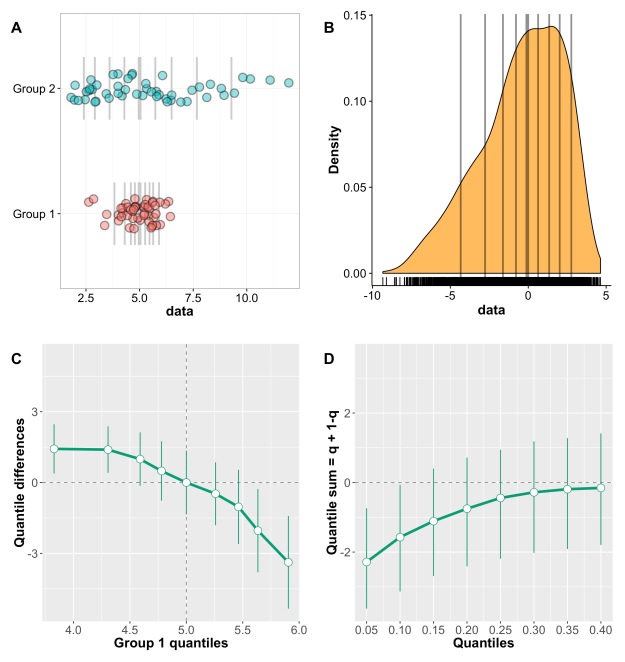
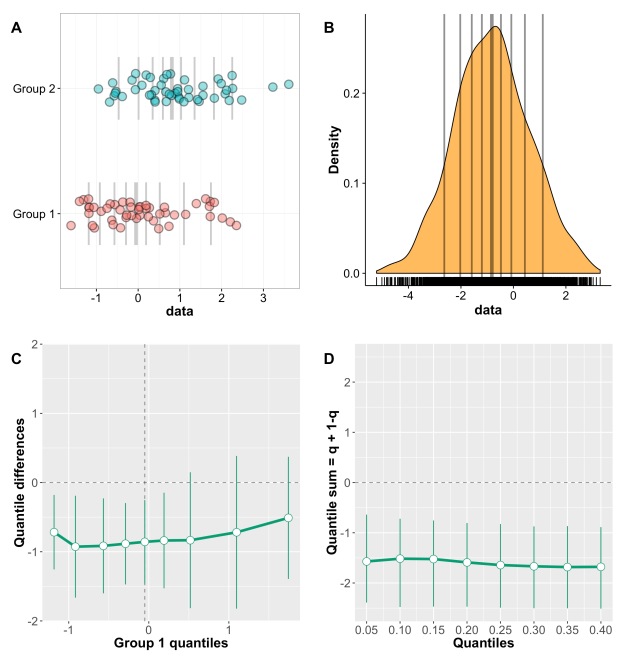
Let’s consider the example presented in Figure 1, in which two groups of participants were tested in two conditions (2 independent x 2 dependent factor design). Panel A illustrates the results using a mean +/- SEM bar graph. An ANOVA on these data reveals a non-significant group effect, a significant main effect of condition, and a significant group x condition interaction. Follow-up paired t-tests reveal a significant condition effect in group 1, but not in group 2. These results seem well supported by the bar graph in Figure 1A. Based on this evidence, it is very common to conclude that group 1 is sensitive to the experimental manipulation, but not group 2. The discussion of the article might even pitch the results in more general terms, making claims about the brain in general.

Figure 1. Different representations of the same behavioural data. Results are in arbitrary units. A Bar graph with mean +/- SEM. B Stripcharts (1D scatterplots) of difference scores. C Stripcharts of linked observations. D Scatterplot of paired observations. The diagonal line has slope 1 and intercept 0. This figure is licensed CC-BY and available on Figshare, along with data and R code to reproduce it (Rousselet 2016a).

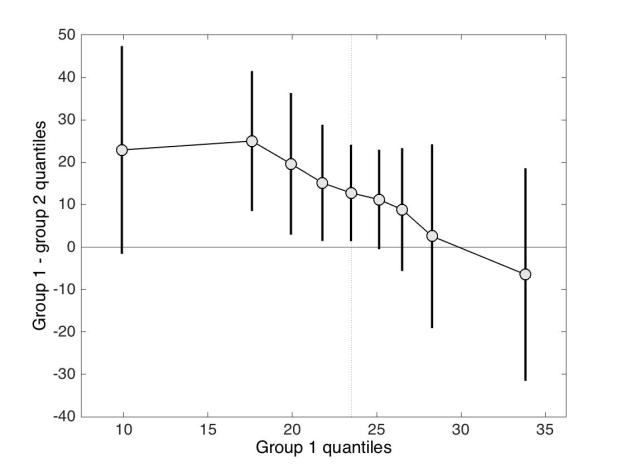
Although the scenario just described is very common in the literature, the conclusions are unwarranted. First, the lack of significance (p<0.05) does not necessarily provide evidence for the lack of effect (Wetzels et al., 2011; Kruschke, 2013). Second, without showing the content of the bars, no conclusion should be drawn at all. So let’s look inside the bars. Figure 1B shows the results from the two independent groups: participants in each group were tested in two conditions, so the pairwise differences are illustrated to reveal the effect sizes and their distributions across participants. The data show large individual differences and overlap between the two distributions. In group 2, except for 2 potential outliers showing large negative effects, the remaining observations are within the range observed in group 1. Six participants from group 2 have differences suggesting an effect in the same direction as group 1, two are near zero, three go in the opposite direction. So, clearly, the lack of significant difference in group 2 is not supported by the data: yes group 2 has overall smaller differences than group 1, but if group 1 is used as a control group, then most participants in group 2 appear to have standard effects. Or so it seems, until we explore the nature of the difference scores by visualising paired observations in each group (Figure 1C). In group 1, as already observed, results in condition 2 are overall larger than in condition 1. In addition, participants with larger scores in condition 1 tend to have proportionally larger differences between conditions 1 and 2. Such relationship seems to be absent in group 2, which suggests that the two groups differ not only in the overall sensitivity to the experimental manipulation, but that other factors could be at play in group 1, and not in group 2. Thus, the group differences might actually be much subtler than suggested by our first analyses. The group dichotomy is easier to appreciate in Figure 1D, which shows a scatterplot of the paired observations in the two groups. In group 1, the majority of paired observations are above the unity line, demonstrating an overall group effect; there is also a positive relationship between the scores in condition 2 and the scores in condition 1. Again, no such relationship seems to be present in group 2. In particular, the two larger negative scores in group 2 are not associated with participants who scored particularly high or low in condition 1, giving us no clue as to the origin of these seemingly outlier scores.

At this stage, we’ve learnt a great deal more about our dataset using detailed graphical representations than relying only on a bar graph and an ANOVA. However, we would need many more than n = 11 participants in both groups to quantify the effects and understand how they differ across groups. We have also not exhausted all the representations that could help us make sense of the results. There is also potentially more to the data, because we haven’t considered the full distribution of single-trials/repetitions. For instance, it is very common to summarise a reaction time distribution of potentially hundreds of trials using a single number, which is then used to perform group analyses. An alternative is to study these distributions in each participant, to understand exactly how they differ between conditions. This single-participant approach would be necessary here to understand how the two groups of participants respond to the experimental manipulation.

In sum, there is much more to the data than what we could conclude from the bar graphs and the ANOVA and t-tests. Once bar graphs and their equivalents are replaced by scatterplots (or boxplots etc.) the story can get much more interesting, subtle, convincing, or the opposite… It depends what surprises the bars are holding. Showing scatterplots is the start of a discussion about the nature of the results, an invitation to go beyond the significant vs. non-significant dichotomy. For the particular results presented in Figure 1, it is rather unclear what is gained by the ANOVA at all compared to detailed graphical representations. Instead of blind statistical significance testing, it would of course be beneficial to properly model the data to make predictions (Kuhn & Johnson, 2013), and to allow integration across subsequent experiments and replication attempts – a critical step that requires Bayesian inference (Verhagen & Wagenmakers, 2014).

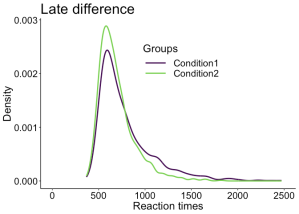
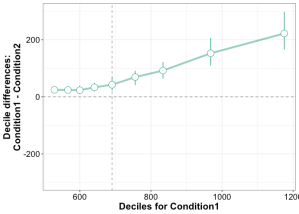
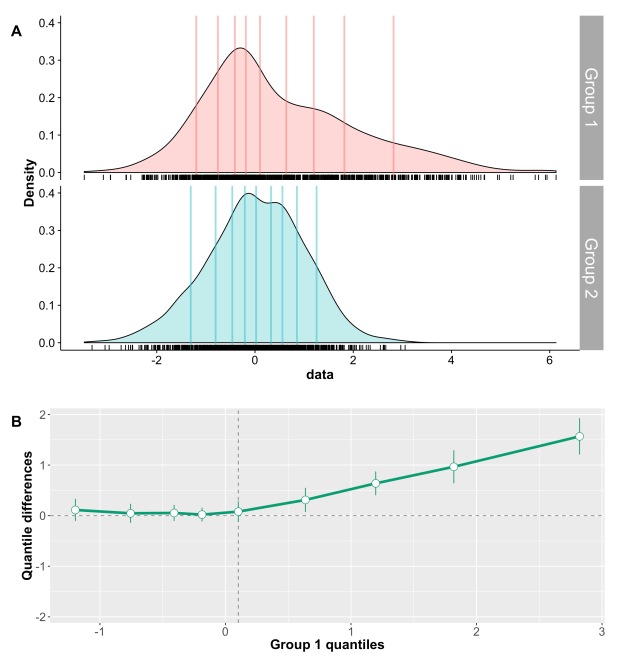
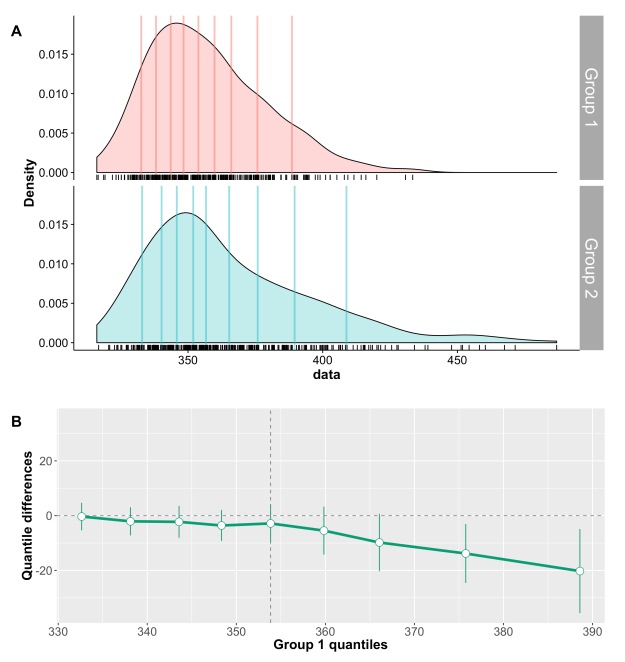
The problems described so far are not limited to relatively simple one dimensional data: they are present in more complex datasets as well, such as EEG and MEG time-series. For instance, it is common to see EEG and MEG evoked responses illustrated using solely the mean across participants (Figure 2A). Although common, this representation is equivalent to a bar graph without error bars/whiskers, and is therefore unacceptable. At a minimum, some measure of uncertainty should be provided, for instance so-called confidence intervals (Figure 2B). Also, because it can be difficult to mentally subtract two time-courses, it is important to illustrate the time-course of the difference as well (Figure 2C). In particular, showing the difference helps to consider all the data, not just large peaks, to avoid underestimating potentially large effects occurring before or after the main peaks. In addition, Figure 2C illustrates ERP differences for every participant – an ERP version of a scatterplot. This more detailed illustration is essential to allow readers to assess effect sizes, inter-participant differences, and ultimately to interpret significant and non-significant results. For instance, in Figure 2C, there is a non-significant group negative difference 100 ms, and a large positive difference 120 to 280 ms. What do they mean? The individual traces reveal a small number of participants with relatively large differences 100 ms despite the lack of significant group effect, and all participants have a positive difference 120 to 250 ms post-stimulus. There are also large individual differences at most time points. So Figure 2C, although certainly not the ultimate representation, offers a much richer and compelling description than the group averages on their own; Figure 2C also suggests that more detailed group analyses would be beneficial, as well as single-participant analyses (Pernet et al., 2011; Rousselet & Pernet, 2011).

MATLAB Handle Graphics

Figure 2. Different representations of the same ERP data.  Paired design in which the same participants saw two image categories. A Standard ERP figure showing the mean across participants for two conditions. B Mean ERPs with 95% confidence intervals. The black dots along the x-axis mark time points at which there is a significant paired t-test (p<0.05).  C Time course of the ERP differences. Differences from individual participants are shown in grey. The mean difference is superimposed using a thick black curve. The thinner black curves mark the mean’s 95% confidence interval. This figure is licensed CC-BY and available on Figshare, along with data and Matlab code to reproduce it (Rousselet 2016b).

To conclude, we urge authors, reviewers and editors to promote and implement these guidelines to achieve higher standards in reporting neuroscience research:

• as much as possible, do not use line and bar graphs; use scatterplots instead, or, if you have large sample sizes, histograms, kernel density plots, or boxplots;

• for paired designs, show distributions of pairwise differences, so that readers can assess how many comparisons go in the same direction as the group, their size, and their variability; this recommendation also applies to brain imaging data, for instance MEEG and fMRI BOLD time-courses;

• report how many participants show an effect in the same direction as the group;

• only draw conclusions about what was assessed: for instance, if you perform a t-test on means, you should only conclude about differences in means, not about group differences in general;

• don’t use a star system to dichotomise p values: p values do not measure effect sizes or the amount of evidence against or in favour of the null hypothesis (Wagenmakers, 2007);

• don’t agonise over p values: focus on detailed graphical representations and robust effect sizes instead (Wilcox, 2006; Wickham, 2009; Allen et al., 2012; Wilcox, 2012; Weissgerber et al., 2015);

• consider Bayesian statistics, to get the tools to align statistical and scientific reasoning (Cohen, 1994; Goodman, 1999; 2016).

Finally, we cannot ignore that using detailed illustrations for potentially complex designs, or designs involving many group comparisons, is not straightforward: research in that direction, including the creation of open-access toolboxes, is of great value to the community, and should be encouraged by funding agencies.

References

Allen, E.A., Erhardt, E.B. & Calhoun, V.D. (2012) Data visualization in the neurosciences: overcoming the curse of dimensionality. Neuron, 74, 603-608.

Anscombe, F.J. (1973) Graphs in Statistical Analysis. Am Stat, 27, 17-21.

Cohen, D. (1994) The earth is round (p<.05). American Psychologist, 49, 997-1003.

Doksum, K. (1974) Empirical Probability Plots and Statistical Inference for Nonlinear Models in the two-Sample Case. Annals of Statistics, 2, 267-277.

Doksum, K.A. & Sievers, G.L. (1976) Plotting with Confidence – Graphical Comparisons of 2 Populations. Biometrika, 63, 421-434.

Gigerenzer, G. (2004) Mindless statistics. Journal of Behavioral and Experimental Economics (formerly The Journal of Socio-Economics), 33, 587-606.

Goodman, S.N. (1999) Toward evidence-based medical statistics. 1: The P value fallacy. Ann Intern Med, 130, 995-1004.

Goodman, S.N. (2016) Aligning statistical and scientific reasoning. Science, 352, 1180-1181.

Kruschke, J.K. (2013) Bayesian estimation supersedes the t test. J Exp Psychol Gen, 142, 573-603.

Kuhn, M. & Johnson, K. (2013) Applied predictive modeling. Springer, New York.

Pernet, C.R., Sajda, P. & Rousselet, G.A. (2011) Single-trial analyses: why bother? Frontiers in psychology, 2, doi: 10.3389-fpsyg.2011.00322.

Rousselet, G.A. & Pernet, C.R. (2011) Quantifying the Time Course of Visual Object Processing Using ERPs: It’s Time to Up the Game. Front Psychol, 2, 107.

Rousselet, G. (2016a). Different representations of the same behavioural data. figshare.
https://dx.doi.org/10.6084/m9.figshare.3504539

Rousselet, G. (2016b). Different representations of the same ERP data. figshare.
https://dx.doi.org/10.6084/m9.figshare.3504566

Verhagen, J. & Wagenmakers, E.J. (2014) Bayesian tests to quantify the result of a replication attempt. J Exp Psychol Gen, 143, 1457-1475.

Wagenmakers, E.J. (2007) A practical solution to the pervasive problems of p values. Psychonomic bulletin & review, 14, 779-804.

Weissgerber, T.L., Milic, N.M., Winham, S.J. & Garovic, V.D. (2015) Beyond bar and line graphs: time for a new data presentation paradigm. PLoS Biol, 13, e1002128.

Wetzels, R., Matzke, D., Lee, M.D., Rouder, J.N., Iverson, G.J. & Wagenmakers, E.J. (2011) Statistical Evidence in Experimental Psychology: An Empirical Comparison Using 855 t Tests. Perspectives on Psychological Science, 6, 291-298.

Wickham, H. (2009) ggplot2 : elegant graphics for data analysis. Springer, New York ; London.

Wilcox, R.R. (2006) Graphical methods for assessing effect size: Some alternatives to Cohen’s d. Journal of Experimental Education, 74, 353-367.

Wilcox, R.R. (2012) Introduction to robust estimation and hypothesis testing. Academic Press, San Diego, CA.

Wilcox, R.R., Erceg-Hurn, D.M., Clark, F. & Carlson, M. (2014) Comparing two independent groups via the lower and upper quantiles. J Stat Comput Sim, 84, 1543-1551.

How to quantify typical differences between distributions

In this post, I describe two complementary lines of enquiry for group comparisons:

(1) How do typical levels compare between groups?

(2.1) for independent groups What is the typical difference between randomly selected members of the two groups?

(2.2) for dependent groups What is the typical pairwise difference?

These two questions can be answered by exploring entire distributions, not just one measure of central tendency.

---

The R code for this post is available on github, and is based on Rand Wilcox’s WRS R package, with extra visualisation functions written using ggplot2. I will describe Matlab code in another post.

---

Independent groups

When comparing two independent groups, the typical approach consists in comparing the marginal distributions using a proxy: each distribution is summarised using one value, usually the non-robust mean. The difference between means is then normalised by some measure of variability – usually involving the non-robust variance, in which case we get the usual t-test. There is of course no reason to use only the mean as a measure of central tendency: robust alternatives such as trimmed means and M-estimators are more appropriate in many situations (Wilcox, 2012a). However, whether we compare the means or the medians or the 20% trimmed means of two groups, we focus on one question:

“How does the typical level/participant in one group compares to the typical level/participant in the other group?” Q1

There is no reason to limit our questioning of the data to the average Joe in each distribution: to go beyond differences in central tendency, we can perform systematic group comparisons using shift functions. Nevertheless, shift functions are still based on a comparison of the two marginal distributions, even if a more complete one.

An interesting alternative approach consists in asking:

“What is the typical difference between any member of group 1 and any member of group 2?” Q2

This approach involves computing all the pairwise differences between groups, as covered previously.

Let’s look at an example. Figure 1A illustrates two independent samples. The scatterplots indicate large differences in spread between the two groups, and also suggest larger differences in the right than the left tails of the distributions. The medians of the two groups appear very similar, so the two distributions do not seem to differ in central tendency. In keeping with these observations, a t-test and a Mann-Whitney-Wilcoxon test are non-significant, but a Kolmogorov-Smirnov test is.

Figure 1. Independent groups: non-uniform shift. A Stripcharts of marginal distributions. Vertical lines mark the deciles, with a thick line for the median. B Kernel density representation of the distribution of difference scores. Vertical lines mark the deciles, with a thick line for the median. C Shift function. Group 1 – group 2 is plotted along the y-axis for each decile (white disks), as a function of group 1 deciles. For each decile difference, the vertical line indicates its 95% bootstrap confidence interval. When a confidence interval does not include zero, the difference is considered significant in a frequentist sense. The 95% confidence intervals are controlled for multiple comparisons. D Difference asymmetry plot with 95% confidence intervals. The family-wise error is controlled by adjusting the critical p values using Hochberg’s method; the confidence intervals are not adjusted.

This discrepancy between tests highlights an important point: if a t-test is not significant, one cannot conclude that the two distributions do not differ. A shift function helps us understand how the two distributions differ (Figure 1C): the overall profile corresponds to two centred distributions that differ in spread; for each decile, we can estimate by how much they differ, and with what uncertainty; finally, the differences appear asymmetric, with larger differences in the right tails.

Is this the end of the story? No, because so far we have only considered Q1, how the two marginal distributions compare. We can get a different but complementary perspective by considering Q2, the typical difference between any member of group 1 and any member of group 2. To address Q2, we compute all the pairwise differences between members of the two groups. In this case each group has n=50, so we end up with 2,500 differences. Figure 1B shows a kernel density representation of these differences. So what does the typical difference looks like? The median of the differences is very near zero, so it seems on average, if we randomly select one observation from each group, they will differ very little. However, the differences can be quite substantial, and with real data we would need to put these differences in context, to understand how large they are, and their physiological/psychological interpretation. The differences are also asymmetrically distributed, with negative skewness: negative scores extend to -10, whereas positive scores don’t even reach +5. This asymmetry relates to our earlier observation of asymmetric differences in the shift function.

Recently, Wilcox (2012) suggested a new approach to quantify asymmetries in difference distributions. To understand his approach, we first need to consider how difference scores are usually characterised. It helps to remember that for continuous distributions, the Mann—Whitney-Wilcoxon U statistics = sum(X>Y) for all pairwise comparisons, i.e. the sum of the number of times observations in group X are larger than observations in group Y. Concretely, to compute U we sum the number of times observations in group X are larger than observations on group Y. This calculation requires to compute all pairwise differences between X and Y, and then count the number of positive differences. So the MWW test assesses P(X>Y) = 0.5. Essentially, the MWW test is a non- parametric test of the hypothesis that the distributions are identical. The MWW test does not compare the medians of the marginal distributions as often stated; also, it estimates the wrong standard error (Cliff, 1996). A more powerful test is Cliff’s delta, which uses P(X>Y) – P(X<Y) as a measure of effect size. As expected, in our current example Cliff’s delta is not significant, because the difference distribution has a median very near zero.

Wilcox’s approach is an extension of the MWW test: the idea is to get a sense of the asymmetry of the difference distribution by computing a sum of quantiles = q + (1-q), for various quantiles estimated using the Harrell-Davis estimator. A percentile bootstrap technique is used to derive confidence intervals. Figure 1D shows the resulting difference asymmetry plot  (Wilcox has not given a clear name to that new function, so I made one up). In this plot, 0.05 stands for the sum of quantile 0.05 + quantile 0.95; 0.10 stands for the sum of quantile 0.10 + quantile 0.90; and so on… The approach is not limited to these quantiles, so sparser or denser functions could be tested too. Figure 1D reveals negative sums of the extreme quantiles (0.05 + 0.95), and progressively smaller, converging to zero sums as we get closer to the centre of the distribution. So the q+(1-q) plot suggests that the two groups differ, with maximum differences in the tails, and no significant differences in central tendency. Contrary to the shift function, the q+(1-q) plot let us conclude that the difference distribution is asymmetric, based on the 95% confidence intervals. Other alpha levels can be assessed too.

In the case of two random samples from a normal population, one shifted by a constant compared to the other, the shift function and the difference asymmetry function should be about flat, as illustrated in Figure 2. In this case, because of random sampling and limited sample size, the two approaches provide different perspectives on the results: the shift function suggests a uniform shift, but fails to reject for the three highest deciles; the difference asymmetry function more strongly suggests a uniform shift, with all sums at about the same value. This shows that all estimated pairs of quantiles are asymmetric about zero, because the difference function is uniformly shifted away from zero.

Figure 2. Independent groups: uniform shift. Two random samples of 50 observations were generated using rnorm. A constant of 1 was added to group 2.

When two distributions do not differ, both the shift function and the difference asymmetry function should be about flat and centred around zero – however this is not necessarily the case, as shown in Figure 3.

Figure 3. Independent groups: no shift – example 1. Two random samples of 50 observations were generated using rnorm.

Figure 4 shows another example in which no shift is present, and with n=100 in each group, instead of n=50 in the previous example.

Figure 4. Independent groups: no shift – example 2.  Two random samples of 100 observations were generated using rnorm.

In practice, the asymmetry plot will often not be flat. Actually, it took me several attempts to generate two random samples associated with such flat asymmetry plots. So, before getting too excited about your results, it really pays to run a few simulations to get an idea of what random fluctuations can look like. This can’t be stressed enough: you might be looking at noise!

Dependent groups

Wilcox & Erceg-Hurn (2012) described a difference asymmetry function for dependent group. We’re going to apply the technique to the dataset presented in Figure 5. Panel A shows the two marginal distributions. However, we’re dealing with a paired design, so it is impossible to tell how observations are linked between conditions. This association is revealed in two different ways in panels B & C, which demonstrate a striking pattern: for participants with weak scores in condition 1, differences tend to be small and centred about zero; beyond a certain level, with increasing scores in condition 1, the differences get progressively larger. Finally, panel D shows the distribution of differences, which is shifted up from zero, with only 6 out of 35 differences inferior to zero.

At this stage, we’ve learnt a lot about our dataset – certainly much more than would be possible from current standard figures. What else do we need? Statistical tests?! I don’t think they are absolutely necessary. Certainly, providing a t-test is of no interest whatsoever if Figure 5 is provided, because it cannot provide information we already have.

Figure 5. Dependent groups: data visualisation. A Stripcharts of the two distributions. Horizontal lines mark the deciles, with a thick line for the median. B Stripcharts of paired observations. Scatter was introduced along the x axis to reveal overlapping observations. C Scatterplot of paired observations. The diagonal black reference line of no effect has slope one and intercept zero. The dashed grey lines mark the quartiles of the two conditions. In panel C, it would also be useful to plot the pairwise differences as a function of condition 1 results. D Stripchart of difference scores. Horizontal lines mark the deciles, with a thick line for the median.

Figure 6 provides quantifications and visualisations of the effects using the same layout as Figure 5. The shift function (Figure 6C) shows a non-uniform shift between the marginal distributions: the first three deciles do not differ significantly, the remaining deciles do, and there is an overall trend of growing differences as we progress towards the right tails of the distributions. The difference asymmetry function provides a different perspective. The function is positive and almost flat, demonstrating that the distribution of differences is uniformly shifted away from zero, a result that cannot be obtained by only looking at the marginal distributions. Of course, when using means comparing the marginals or assessing the difference scores give the same results, because the difference of the means is the same as the mean of the differences. That’s why a paired t-test is the same as a one-sample test on the pairwise differences. With robust estimators the two approaches differ: for instance the difference between the medians of the marginals is not the same as the median of the differences.

Figure 6. Dependent groups: uniform difference shift. A Stripcharts of marginal distributions. Vertical lines mark the deciles, with a thick line for the median. B Kernel density representation of the distribution of difference scores. Horizontal lines mark the deciles, with a thick line for the median. C Shift function. D Difference asymmetry plot with 95% confidence intervals.

As fancy as Figure 6 can be, it still misses an important point: nowhere do we see the relationship between condition 1 and condition 2 results, as shown in panels B & C of Figure 5. This is why detailed illustrations are absolutely necessary to make sense of even the simplest datasets.

If you want to make more inferences about the distribution of differences, as shown in Figure 6B, Figure 7 shows a complementary description of all the deciles with their 95% confidence intervals. These could be substituted with highest density intervals or credible intervals for instance.

Figure 7. Dependent groups: deciles of the difference distribution. Each disk marks a difference decile, and the horizontal green line makes its 95% percentile bootstrap confidence interval. The reference line of no effect appears as a continuous black line. The dashed black line marks the difference median.

Finally, in Figure 8 we look at an example of a non-uniform difference shift. Essentially, I took the data used in Figure 6, and multiplied the four largest differences by 1.5. Now we see that the 9th decile does not respect the linear progression suggested by previous deciles, (Figure 8, panels A & B), and the difference asymmetry function suggests an asymmetric shift of the difference distribution, with larger discrepancies between extreme quantiles.

Figure 8. Dependent groups: non-uniform difference shift. A Stripchart of difference scores. B Deciles of the difference distribution. C Difference asymmetry function.

Conclusion

The techniques presented here provide a very useful perspective on group differences, by combining detailed illustrations and quantifications of the effects. The different techniques address different questions, so which technique to use depends on the question you want to ask. This choice should be guided by experience: to get a good sense of the behaviour of these techniques will require a lot of practice with various datasets, both real and simulated. If you follow that path, you will soon realise that classic approaches such as t-tests on means combined with bar graphs are far too limited, and can hide rich information about a dataset.

I see three important developments for the approach outlined here:

• to make it Bayesian, or at least p value free using highest density intervals;

• to extend it to multiple group comparisons (the current illustrations don’t scale up very easily);

• to extend it to ANOVA type designs with interaction terms.

References

Cliff, N. (1996) Ordinal methods for behavioral data analysis. Erlbaum, Mahwah, N.J.

Wilcox, R.R. (2012a) Introduction to robust estimation and hypothesis testing. Academic Press, San Diego, CA.

Wilcox, R.R. (2012b) Comparing Two Independent Groups Via a Quantile Generalization of the Wilcoxon-Mann-Whitney Test. Journal of Modern Applied Statistical Methods, 11, 296-302.

Wilcox, R.R. & Erceg-Hurn, D.M. (2012) Comparing two dependent groups via quantiles. J Appl Stat, 39, 2655-2664.

the shift function: a powerful tool to compare two entire distributions

 

---

The R code for this post is available on github, and is based on Rand Wilcox’s WRS R package, with extra visualisation functions written using ggplot2. The R code for the 2013 percentile bootstrap version of the shift function was also covered here and here. Matlab code is described in another post.

---

UPDATE: The shift function and its cousin the difference asymmetry function are described in a review article with many examples. And a Bayesian shift function is now available! The hierarchical shift function provides a powerful alternative to the t-test.

---

In neuroscience & psychology, group comparison is usually an exercise that involves comparing two typical observations. This is most of the time achieved using a t-test on means. This standard procedure makes very strong assumptions:

• the distributions differ only in central tendency, not in other aspects;
• the typical observation in each distribution can be summarised by the mean;
• the t-test is sufficient to detect changes in location.

As we saw previously, t-tests on means are not robust. In addition, there is no reason a priori to assume that two distributions differ only in the location of the bulk of the observations. Effects can occur in the tails of the distributions too: for instance a particular intervention could have an effect only in animals with a certain hormonal level at baseline; a drug could help participants with severe symptoms, but not others with milder symptoms… Because effects are not necessarily homogenous among participants, it is useful to have appropriate tools at hand, to determine how, and by how much, two distributions differ. Here we’re going to consider a powerful family of tools that are robust and let us compare entire distributions: shift functions.

A more systematic way to characterise how two independent distributions differ was originally proposed by Doksum (Doksum, 1974; Doksum & Sievers, 1976; Doksum, 1977): to plot the difference between the quantiles of two distributions as a function of the quantiles of one group. The original shift function approach is implemented in the functions sband and wband in Rand Wilcox’s WRS R package.

In 1995, Wilcox proposed an alternative technique which has better probability coverage and potentially more power than Doksum & Sievers’ approach. Wilcox’s technique:

• uses the Harrell-Davis quantile estimator;
• computes confidence intervals of the decile differences with a bootstrap estimation of the standard error of the deciles;
• controls for multiple comparisons so that the type I error rate remains around 0.05 across the 9 confidence intervals. This means that the confidence intervals are a bit larger than what they would be if only one decile was compared, so that the long-run probability of a type I error across all 9 comparisons remains near 0.05;
• is implemented in the shifthd function.

Let’s start with an extreme and probably unusual example, in which two distributions differ in spread, not in location (Figure 1). In that case, any test of central tendency will fail to reject, but it would be wrong to conclude that the two distributions do not differ. In fact, a Kolmogorov-Smirnov test reveals a significant effect, and several measures of effect sizes would suggest non-trivial effects. However, a significant KS test just tells us that the two distributions differ, not how.

Figure 1. Two distributions that differ in spread A Kernel density estimates for the groups. B Shift function. Group 1 – group 2 is plotted along the y-axis for each decile (white disks), as a function of group 1 deciles. For each decile difference, the vertical line indicates its 95% bootstrap confidence interval. When a confidence interval does not include zero, the difference is considered significant in a frequentist sense.

The shift function can help us understand and quantify how the two distributions differ. The shift function describes how one distribution should be re-arranged to match the other one: it estimates how and by how much one distribution must be shifted. In Figure 1, I’ve added annotations to help understand the link between the KDE in panel A and the shift function in panel B. The shift function shows the decile differences between group 1 and group 2, as a function of group 1 deciles. The deciles for each group are marked by coloured vertical lines in panel A. The first decile of group 1 is slightly under 5, which can be read in the top KDE of panel A, and on the x-axis of panel B. The first decile of group 2 is lower. As a result, the first decile difference between group 1 and group 2 is positive, as indicated by a positive value around 0.75 in panel B, as marked by an upward arrow and a + symbol. The same symbol appears in panel A, linking the deciles from the two groups: it shows that to match the first deciles, group 2’s first decile needs to be shifted up. Deciles 2, 3 & 4 show the same pattern, but with progressively weaker effect sizes. Decile 5 is well centred, suggesting that the two distributions do not differ in central tendency. As we move away from the median, we observe progressively larger negative differences, indicating that to match the right tails of the two groups, group 2 needs to be shifted to the left, towards smaller values – hence the negative sign.

To get a good understanding of the shift function, let’s look at its behaviour in several other clear-cut situations. First, let’s consider a  situation in which two distributions differ in location (Figure 2). In that case, a t-test is significant, but again, it’s not the full story. The shift function looks like this:

Figure 2. Complete shift between two distributions

What’s happening? All the differences between deciles are negative and around -0.45. Wilcox (2012) defines such systematic effect has the hallmark of a completely effective method. In other words, there is a complete and seemingly uniform shift between the two distributions.

In the next example (Figure 3), only the right tails differ, which is captured by significant differences for deciles 6 to 9. This is a case described by Wilcox (2012) as involving a partially effective experimental manipulation.

Figure 3. Positive right tail shift

Figure 4 also shows a right tail shift, this time in the negative direction. I’ve also scaled the distributions so they look a bit like reaction time distributions. It would be much more informative to use shift functions in individual participants to study how RT distributions differ between conditions, instead of summarising each distribution by its mean (sigh)!

Figure 4. Negative right tail shift

Figure 5 shows two large samples drawn from a standard normal population. As expected, the shift function suggests that we do not have enough evidence to conclude that the two distributions differ. The shift function does look bumpy tough, potentially suggesting local differences – so keep that in mind when you plug-in your own data.

Figure 5. No difference?

And be careful not to over-interpret the shift function: the lack of significant differences should not be used to conclude that we have evidence for the lack of effect; indeed, failure to reject in the frequentist sense can still be associated with non-trivial evidence against the null – it depends on prior results (Wagenmakers, 2007).

So far, we’ve looked at simulated examples involving large sample sizes. We now turn to a few real-data examples.

Doksum & Sievers (1976) describe an example in which two groups of rats were kept in an environment with or without ozone for 7 days and their weight gains measured (Figure 6). The shift function suggests two results: overall, ozone reduces weight gain; ozone might promote larger weight gains in animals gaining the most weight. However, these conclusions are only tentative given the small sample size, which explains the large confidence intervals.

Figure 6. Weight gains A Because the sample sizes are much smaller than in the previous examples, the distributions are illustrated using 1D scatterplots. The deciles are marked by grey vertical lines, with lines for the 0.5 quantiles. B Shift function.

Let’s consider another example used in (Doksum, 1974; Doksum, 1977), concerning the survival time in days of 107 control guinea pigs and 61 guinea pigs treated with a heavy dose of tubercle bacilli (Figure 7). Relative to controls, the animals that died the earliest tended to live longer in the treatment group, suggesting that the treatment was beneficial to the weaker animals (decile 1). However, the treatment was harmful to animals with control survival times larger than about 200 days (deciles 4-9). Thus, this is a case where the treatment has very different effects on different animals. As noted by Doksum, the same experiment was actually performed 4 times, each time giving similar results.

Figure 7. Survival time

Shift function for dependent groups

All the previous examples were concerned with independent groups. There is a version of the shift function for dependent groups implemented in shiftdhd. We’re going to apply it to ERP onsets from an object detection task (Bieniek et al., 2015). In that study, 74 of our 120 participants were tested twice, to assess the test-retest reliability of different measurements, including onsets. Typically, test-retest assessment is performed using a correlation. However, we care about the units (ms), which a correlation would get rid of, and we had a more specific hypothesis, which a correlation cannot test; so we used a shift function (Figure 8). If you look at the distributions of onsets across participants, you will see that it is overall positively skewed, and with a few participants with particularly early or late onsets. With the shift function, we wanted to test for the overall reliability of the results, but also in particular the reliability of the left and right tails: if early onsets in session 1 were due to chance, we would expect session 2 estimates to be overall larger (shifted to the right); similarly, if late onsets in session 1 were due to chance, we would expect session 2 estimates to be overall smaller (shifted to the left). The shift function does not provide enough evidence to suggest a uniform or non-uniform shift – but we would probably need many more observations to make a strong claim.

Figure 8. ERP onsets

Because we’re dealing with a paired design, the illustration of the marginal distributions in Figure 8 is insufficient: we should illustrate the distribution of pairwise differences too, as shown in Figure 9.

Figure 9. ERP onsets with KDE of pairwise differences

Figure 10 provides an alternative representation of the distribution of pairwise differences using a violin plot.

Figure 10. ERP onsets with violin plot of pairwise differences

Figure 11 uses a 1D scatterplot (strip chart).

Figure 11. ERP onsets with 1D scatterplot of pairwise differences

Shift function for other quantiles

Although powerful, Wilcox’s 1995 technique is not perfect, because it:

• is limited to the deciles;
• can only be used with alpha = 0.05;
• does not work well with tied values.

More recently, Wilcox’s proposed a new version of the shift function that uses a straightforward percentile bootstrap (Wilcox & Erceg-Hurn, 2012; Wilcox et al., 2014). This new approach:

• allows tied values;
• can be applied to any quantile;
• can have more power when looking at extreme quantiles (<=0.1, or >=0.9).
• is implemented in qcomhd for independent groups;
• is implemented in Dqcomhd for dependent groups.

Examples are provided in the R script for this post.

In the percentile bootstrap version of the shift function, p values are corrected, but not the confidence intervals. For dependent variables, Wilcox & Erceg-Hurn (2012) recommend at least 30 observations to compare the .1 or .9 quantiles. To compare the quartiles, 20 observations appear to be sufficient. For independent variables, Wilcox et al. (2014) make the same recommendations made for dependent groups; in addition, to compare the .95 quantiles, they suggest at least 50 observations per group.

Conclusion

The shift function is a powerful tool that can help you better understand how two distributions differ, and by how much. It provides much more information than the standard t-test approach.

Although currently the shift function only applies to two groups, it can in theory be extended to more complex designs, for instance to quantify interaction effects.

Finally, it would be valuable to make a Bayesian version of the shift function, to focus on effect sizes, model the data, and integrate them with other results.

References

Bieniek, M.M., Bennett, P.J., Sekuler, A.B. & Rousselet, G.A. (2015) A robust and representative lower bound on object processing speed in humans. The European journal of neuroscience.

Doksum, K. (1974) Empirical Probability Plots and Statistical Inference for Nonlinear Models in the two-Sample Case. Annals of Statistics, 2, 267-277.

Doksum, K.A. (1977) Some graphical methods in statistics. A review and some extensions. Statistica Neerlandica, 31, 53-68.

Doksum, K.A. & Sievers, G.L. (1976) Plotting with Confidence – Graphical Comparisons of 2 Populations. Biometrika, 63, 421-434.

Wagenmakers, E.J. (2007) A practical solution to the pervasive problems of p values. Psychonomic bulletin & review, 14, 779-804.

Wilcox, R.R. (1995) Comparing Two Independent Groups Via Multiple Quantiles. Journal of the Royal Statistical Society. Series D (The Statistician), 44, 91-99.

Wilcox, R.R. (2012) Introduction to robust estimation and hypothesis testing. Academic Press, Amsterdam; Boston.

Wilcox, R.R. & Erceg-Hurn, D.M. (2012) Comparing two dependent groups via quantiles. J Appl Stat, 39, 2655-2664.

Wilcox, R.R., Erceg-Hurn, D.M., Clark, F. & Carlson, M. (2014) Comparing two independent groups via the lower and upper quantiles. J Stat Comput Sim, 84, 1543-1551.